最简单的R程序实例-拟合线性回归分析¶

一、先看结果¶

二、再看源代码¶

age <- c(1,3,5,2,11,9,3,9,12,3)
weight <- c(4.4,5.3,7.2,5.2,8.5,7.3,6.0,10.4,10.2,6.1)
mean(weight)
sd(weight)
cor(age,weight)

plot(age,weight)
data1=data.frame(x=age,y=weight)  #数据存入数据框
lm.data1<-lm(y ~ x,data=data1)
summary(lm.data1)        #输出拟合后信息
abline(lm.data1,col="red")  # 画图：拟合线性函数

代码详解：

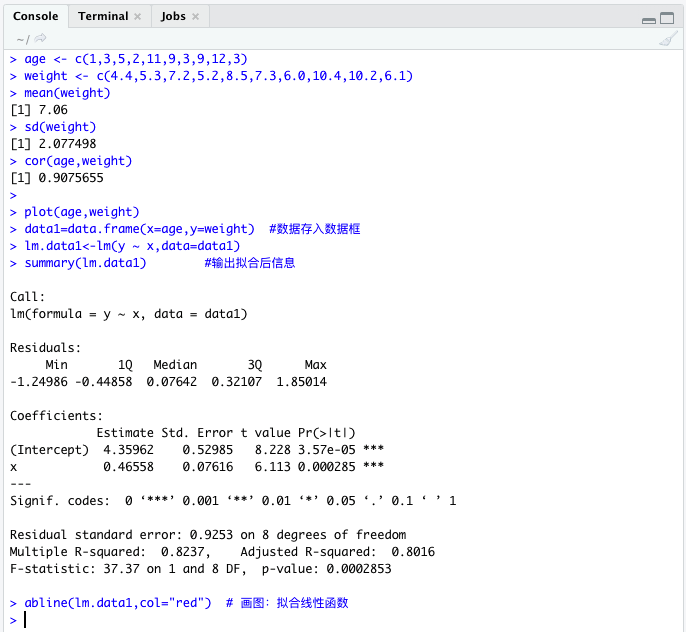
1~2行，设置数据集。

3：计算weight的平均值

4：计算weight的标准差

5：计算age与weight的相关系数（相关系数在0~1之间，越靠近1，相关性越大）

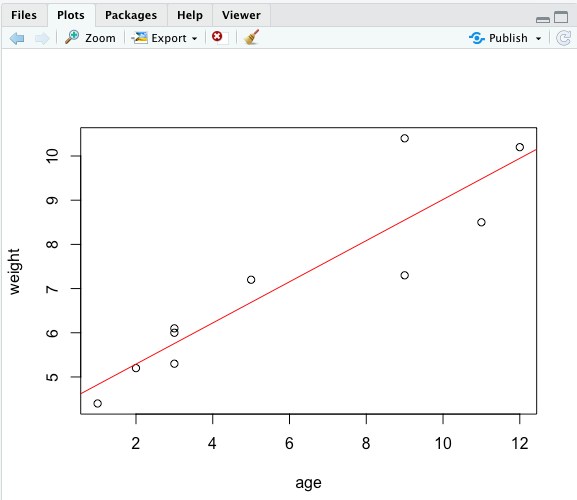
7：基于age与weight绘制散点图

8：将age与weight存入数据框

9：使用lm函数（后面详解）

10：输入拟合后的汇总信息

11：绘制拟合线

三、函数详解¶

`lm()` 函数¶

lm(formula, data, subset, weights, na.action,
   method = "qr", model = TRUE, x = FALSE, y = FALSE, qr = TRUE,
   singular.ok = TRUE, contrasts = NULL, offset, ...)

formula代表拟合的公式，如Y ~ X，则表示：对因变量Y和自变量X作线性拟合拟合模型为

y = a + bx

lm对象即lm函数返回的值，其属性包括：（控制台输出结果）

> x <- 1:10
> y <- rnorm(10)
> line.model <- lm(y~x)
> names(line.model)
[1] "coefficients"  "residuals"     "effects"       "rank"          "fitted.values"
[6] "assign"        "qr"            "df.residual"   "xlevels"       "call"
[11] "terms"         "model"

常用的有coefficients，residuals和fitted.values，分别表示拟合的得到的各系数的值、残差和预测值。

> line.model$coefficients
(Intercept)           x
-0.08691011 -0.07748115
> line.model$residuals
          1           2           3           4           5           6           7           8           9          10
-0.99596463  1.35205887 -0.96315519  0.10319393  0.13748375  0.01977122  1.46849910 -0.35369933 -0.19446886 -0.57371887
> line.model$fitted.values
         1          2          3          4          5          6          7          8          9         10
-0.1643913 -0.2418724 -0.3193536 -0.3968347 -0.4743159 -0.5517970 -0.6292782 -0.7067593 -0.7842405 -0.8617216

可以看出该拟合曲线为y=-0.08691011 -0.07748115x

其他值的调用，包括p值，给定x预测的y值，拟合系数R方等需要通过summary函数调用，例如：

1. 计算p值¶

> f <- summary(line.model)$fstatistic
> pf(f[1], f[2], f[3], lower.tail=F)
    value
0.4549477

给定x预测相应的y值（给定0，1，2 预测出的预测值如下）

> predict(line.model, data.frame(x=c(0, 1, 2)))
          1           2           3
-0.08691011 -0.16439126 -0.24187241

2. 拟合系数R平方¶

> summary(line.model)$r.squared
[1] 0.07155641
> summary(line.model)$adj.r.squared
[1] -0.04449903

也可以直接通过 summary(line.model) 打印出大部分与回归直线相关的一些结果

> summary(line.model)

Call:
lm(formula = y ~ x)

Residuals:
     Min       1Q   Median       3Q      Max
-0.99596 -0.51871 -0.08735  0.12891  1.46850

Coefficients:
            Estimate Std. Error t value Pr(>|t|)
(Intercept) -0.08691    0.61226  -0.142    0.891
x           -0.07748    0.09867  -0.785    0.455

Residual standard error: 0.8963 on 8 degrees of freedom
Multiple R-squared:  0.07156,   Adjusted R-squared:  -0.0445
F-statistic: 0.6166 on 1 and 8 DF,  p-value: 0.4549